I am thrilled to release fast.ai’s newest free course, Computational Linear Algebra, including an online textbook and a series of videos, and covering applications (using Python) such as how to identify the foreground in a surveillance video, how to categorize documents, the algorithm powering Google’s search, how to reconstruct an image from a CT scan, and more.
Jeremy and I developed this material for a numerical linear algebra course we taught in the University of San Francisco’s Masters of Analytics program, and it is the first ever numerical linear algebra course, to our knowledge, to be completely centered around practical applications and to use cutting edge algorithms and tools, including PyTorch, Numba, and randomized SVD. It also covers foundational numerical linear algebra concepts such as floating point arithmetic, machine epsilon, singular value decomposition, eigen decomposition, and QR decomposition.
What is numerical linear algebra?
“What exactly is numerical linear algebra?” you may be wondering. It is all about getting computers to do matrix math with speed and with acceptable accuracy, and way more awesome than the somewhat dull name suggests. Who cares about how computers do matrix math? All of you, probably. Data science is largely about manipulating matrices since almost all data can be represented as a matrix: time-series, structured data, anything that fits in a spreadsheet or SQL database, images, and language (often represented as word embeddings).
A typical first linear algebra course focuses on how to solve matrix problems by hand, for instance, spending time using Gaussian Elimination with pencil and paper to solve a small system of equations manually. However, it turns out that the methods and concerns for solving larger matrix problems via a computer are often drastically different:
Speed: when you have big matrices, matrix computations can get very slow. There are different ways of addressing this:
- Different algorithms: there may be a less intuitive way to solve the problem that still gets the right answer, and does it faster.
- Vectorizing or parallelizing your code.
- Locality: traditional runtime computations focus on Big O, the number of operations computed. However, for modern computing, moving data around in memory can be very time-consuming, and you need ways to minimize how much memory movement you do.
Accuracy: Computers represent numbers (which are continuous and infinite) in a discrete and finite way, which means that they have limited accuracy. Rounding errors can add up, particularly if you are iterating! Furthermore, some math problems are not very stable, meaning that if you vary the input a little, you get a vastly different output. This isn’t a problem with rounding or with the computer, but it can still have a big impact on your results.
Memory use: for matrices that have lots of zero entries, or that have a particular structure, there are more efficient ways to store these in memory.
Scalability: in many cases you are interested in working with more data than you have space in memory for.
This course also includes some very modern approaches that we don’t know of any other numerical linear algebra courses covering (and we have done a lot of researching of numerical linear algebra courses and syllabi), such as:
- Randomized algorithms
- Numba: a library that compiles Python to optimized C code
- PyTorch: an alternative to Numpy that runs on the GPU (also, an excellent deep learning framework, although we are using it just as a Numpy alternative here to speed up our code)
Basically, we considered anything that could speed up your matrix computations as fair game to cover here!
Teaching Methodology
This course uses the same top down, code first, application centered teaching method as we used in our Practical Deep Learning for Coders course, and which I describe in more detail in this blog post and this talk I gave at the San Francisco Machine Learning meetup. Basically, our goal is to get students working on interesting applications as quickly as possible, and then to dig into the underlying details later as time goes on.
This approach is very different from how most math courses operate: typically, math courses first introduce all the separate components you will be using, and then you gradually build them into more complex structures. The problems with this are that students often lose motivation, don’t have a sense of the “big picture”, and don’t know which pieces they’ll even end up needing. We have been inspired by Harvard professor David Perkin’s baseball analogy. We don’t require kids to memorize all the rules of baseball and understand all the technical details before we let them have fun and play the game. Rather, they start playing with a just general sense of it, and then gradually learn more rules/details as time goes on. All that to say, don’t worry if you don’t understand everything at first! You’re not supposed to. We will start using some “black boxes” or matrix decompositions that haven’t yet been explained, and then we’ll dig into the lower level details later.
I love math (I even have a math PhD!), but when I’m trying to solve a practical problem, code is more useful than theory. Also, one of the tests of whether you truly understand something is if you can code it, so this course if much more code-centered than a typical numerical linear algebra course.
The Details
The primary resource for this course is the free online textbook of Jupyter Notebooks, available on Github. They are full of explanations, code samples, pictures, interesting links, and exercises for you to try. Anyone can view the notebooks online by clicking on the links in the readme Table of Contents. However, to really learn the material, you need to interactively run the code, which requires installing Anaconda on your computer (or an equivalent set up of the Python scientific libraries) and you will need to be able to clone or download the git repo.
Accompanying the notebooks is a playlist of lecture videos, available on YouTube. If you are ever confused by a lecture or it goes too quickly, check out the beginning of the next video, where I review concepts from the previous lecture, often explaining things from a new perspective or with different illustrations.
You can ask questions or share your thoughts and resources using the Computational Linear Algebra category on our fast.ai discussion forums.
This course assumes more background than our Practical Deep Learning for Coders course. It was originally taught during the final term before graduation of the USF Master of Science in Analytics program, and all students had already participated in a “Linear Algebra Bootcamp”. If you are new to linear algebra, I recommend you watch the beautiful 3Blue 1Brown Essence of Linear Algebra video series as preparation.
There is no official registration for the course; rather it is up to you to work through the materials at your own pace. You can get started now, by watching the 1st video:
Applications covered
This list is not exhaustive, but here are a few of the applications covered:
How to identify the foreground in a surveillance video, by decomposing a matrix into the sum of two other matrices

Photo = Background + People
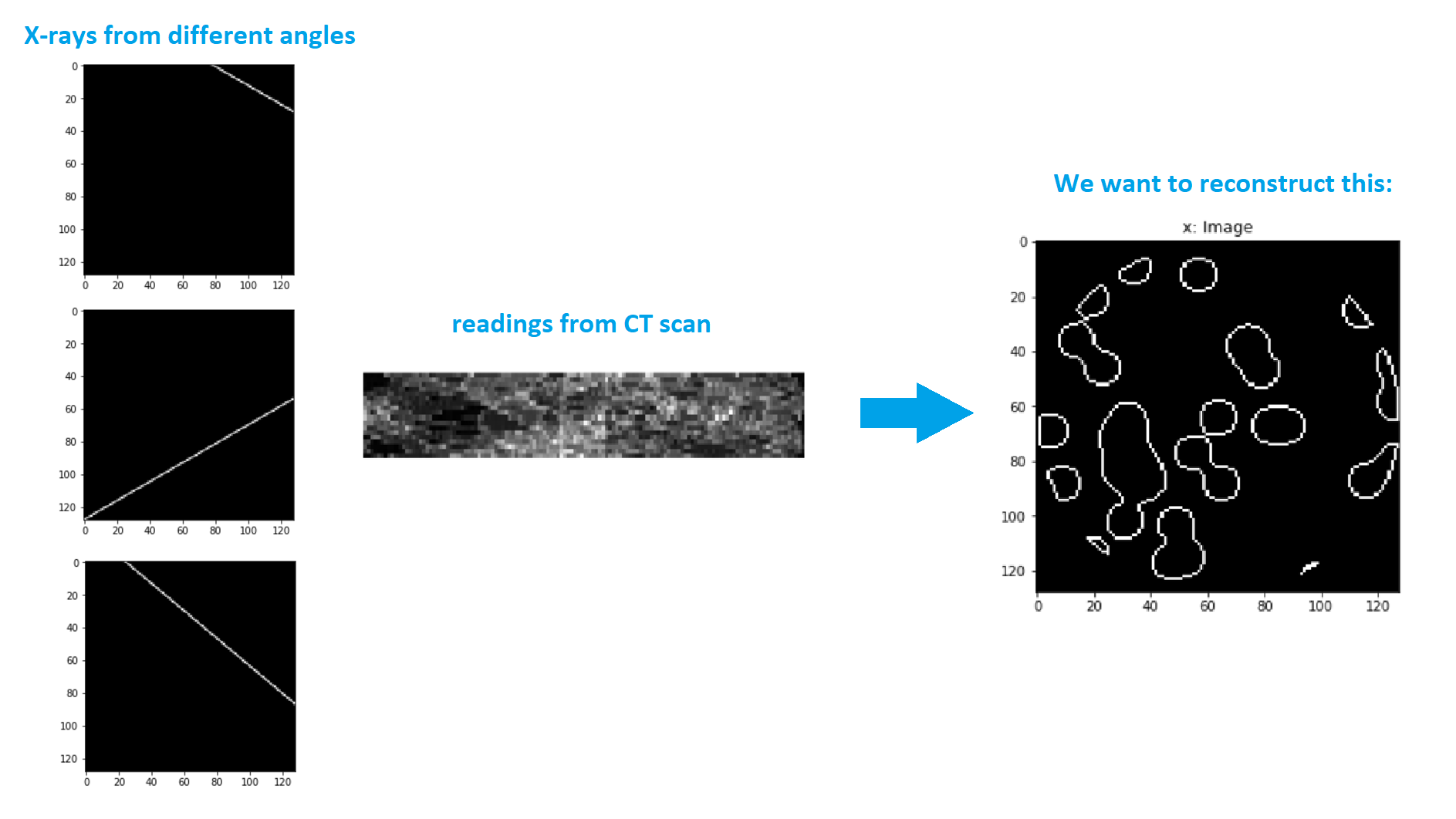
How to reconstruct an image from a CT scan using the angles of the x-rays and the readings (spoiler: it’s surprisingly simple and we use linear regression!), covered in Lesson 4
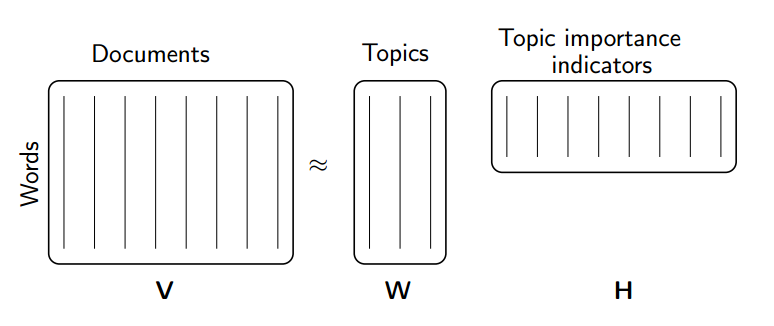
- How to identify topics in a corpus of documents, covered in Lesson 2.
- The algorithm behind Google’s PageRank, used to rank the relative importance of different web pages
Can’t I just use sci-kit learn?
Many (although certainly not all) of the algorithms covered in this course are already implemented in scientific Python libraries such as Numpy, Scipy, and Scikit Learn, so you may be wondering why it’s necessary to learn what’s going on underneath the hood. Knowing how these algorithms are implemented will allow you to better combine and utilize them, and will make it possible for you to customize them if needed. In at least one case, we show how to get a sizable speedup over sci-kit learn’s implementation of a method. Several of the topics we cover are areas of active research, and there is recent research that has not yet been added to existing libraries.